斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
leetcode 509
- 带memo的递归
class Solution:
def fib(self, N: int) -> int:
memo = {}
def recur(n):
if n <=1:return n
if n in memo:
return memo[n]
return recur(n-1)+recur(n-2)
return recur(N)
- 动态规划
class Solution:
def fib(self, n: int) -> int:
if n <=1:return n
vals = [0]*(n+1)
vals[1] = 1
for i in range(2,n+1):
vals[i] = vals[i-1] + vals[i-2]
return vals[n] % 1000000007
青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2
输出:2
示例 2:
输入:n = 7
输出:21
提示:
0 <= n <= 100
- 与斐波那契数列一样
class Solution:
def numWays(self, n: int) -> int:
if n < 2:return 1
dp = [0] * (n+1)
dp[0],dp[1] = 1,1
for i in range(2,n+1):
dp[i] = (dp[i-1] + dp[i-2])%1000000007
return dp[n]
变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
- 相对于上一题,第n阶台阶只能由第n-1和n-2阶得到,这道题中从任意一阶台阶都能一步到n阶,所以$f(n)=\sum_{i=0}^{n-1}f(i)$
class Solution:
def jumpFloorII(self, number):
if number <2:return 1
dp = [0] * (number +1)
dp[0],dp[1] = 1,1
for i in range(2,number+1):
for j in range(0,i):
dp[i] += dp[j]
return dp[number]
矩形覆盖
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
比如n=3时,2*3的矩形块有3种覆盖方法:
- 实质也是斐波那契数列,2*n时只需要考虑
2(n-1)和2(n-2)的结果,最左边是2*1或者2*2的矩形,其他情况均是重复情况。
class Solution:
def rectCover(self, number):
if number <= 1:return number
dp = [0] * (number + 1)
dp[1],dp[2] = 1,2
for i in range(3,number+1):
dp[i]=dp[i-1]+dp[i-2]
return dp[number]
剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问k[0]*k[1]*...*k[m-1]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
- 动态规划思路:对于一条长为n的绳子,至少要划分两截,其最大乘积的值等同于:先从区间$[1,n-1]$去一个长度
i,然后再对n-i寻找其最大乘积长度(即最优子结构),计算乘积后最大的那个即为长为n的绳子对应的结果。由于可以直接分为两截,在进行比较时需要考虑直接分为两截i和n-i时的乘积与继续对n-i的绳子继续划分的乘积。
class Solution:
def integerBreak(self, n: int) -> int:
if n <= 2:return 1
dp = [1 for _ in range(n+1)]
for i in range(2,n+1):
res= 0
for j in range(1,i):
res =max(res,j*(i-j),j*dp[i-j])
dp[i]=res
return dp[n]
*丑数
我们把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
示例:
输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
1 是丑数。
n 不超过1690。
- 分析:不能直接遍历所有数并验证其是不是丑数,时间消耗过大,而是根据丑数的规律,由得出来的丑数推理出后续的丑数。
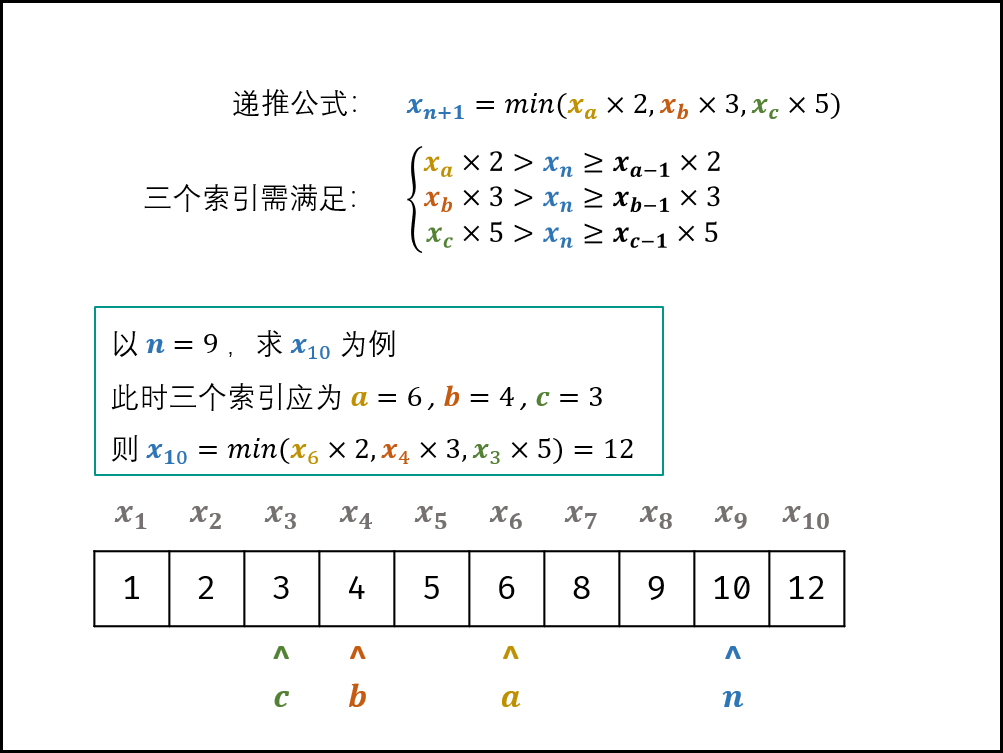
class Solution:
def nthUglyNumber(self, n: int) -> int:
dp, a, b, c = [1] * n, 0, 0, 0
for i in range(1, n):
n2, n3, n5 = dp[a] * 2, dp[b] * 3, dp[c] * 5
dp[i] = min(n2, n3, n5)
if dp[i] == n2: a += 1
if dp[i] == n3: b += 1
if dp[i] == n5: c += 1
return dp[-1]
leetcode 1025:除数博弈
爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作:
选出任一 x,满足 0 < x < N 且 N % x == 0 。 用 N - x 替换黑板上的数字 N 。 如果玩家无法执行这些操作,就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 false。假设两个玩家都以最佳状态参与游戏。
示例 1:
输入:2
输出:true
解释:爱丽丝选择 1,鲍勃无法进行操作。
示例 2:
输入:3
输出:false
解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
提示:
1 <= N <= 1000
- 状态转移: 如果 i 的约数里面有存在为
False的(即输掉的情况),则当前 i 应为True;如果没有,则为False。
class Solution:
def divisorGame(self, N: int) -> bool:
if N<=1:return False
dp = [0] * (N+1)
dp[2] = 1
for i in range(3,N+1):
for j in range(1,i//2):
# 若j是i的余数且dp[i-j]为假(0)的话,则代表当前为真(1)
if i%j==0 and dp[i-j] == 0:
dp[i] = 1
break
return dp[N]
leetcode 198:打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
0 <= nums.length <= 1000 <= nums[i] <= 400
思路:当i<=2时,能偷取的最大值为f(i)=max(nums[0].nums[1])。当i=3时,有两种选择:(1)选择偷取当前位置i处的房屋,则无法偷取i-1处的房屋,其在i处的最大值为nums[i]+max(f(j)),j的范围为$[0,i-2]$ 。(2) 不偷取该处,则还需要再比较f(i-1)处的结果。
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
elif n == 1:return nums[0]
dp = [0] * (n)
dp[0] = nums[0]
dp[1] = max(nums[0:2])
for i in range(2,n):
for j in range(i-1):
dp[i] = max(dp[i],nums[i]+dp[j])
dp[i] = max(dp[i],dp[i-1])
return dp[-1]
leetcode 53:最大子序列和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
- 状态
f(i)为以第i个单词结尾的最大和,其状态转移方程为:f(i)=max(f(i-1)+nums[i],nums[i]),因为题目要求为连续子数组,所以其最大和要么是上一个的最大和加上当前的值,或者是从改值重新计算和。
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
if n == 0:return 0
pre,res=0,nums[0]
for i in range(0,n):
pre = max(nums[i],pre+nums[i])
res = max(res,pre)
return res
leetcode 322: 零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
说明:
你可以认为每种硬币的数量是无限的。
- 动态规划:初始条件:coins数组中的金额为1.
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if amount ==0:return 0
dp = [-1]*(amount+1)
for val in coins:
if val <= amount:
dp[val] = 1
for i in range(1,amount+1):
for j in coins:
if i - j < 0 or dp[i-j]==-1:
continue
dp[i] = min(dp[i],dp[i-j]+1) if dp[i]!=-1 else dp[i-j]+1
return dp[amount]
leetcode 120: 三角形最小路径和
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
- 使用动态规划时边界不好控制,因此通过带备忘录的递归来实现,
f(0,0)=min(f(1,0),f(1,1))+num[0,0]. - 注意:初始化
memo时尽量避免用*len()的方法,会出现浅拷贝时多个子list同时更新的问题。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if not triangle or not triangle[0]:return 0
#self.memo = [[None]*len(triangle[-1])]*len(triangle)
self.memo = [[-1]*len(triangle[-1]) for _ in range(len(triangle))]
return self.find(triangle,0,0)
def find(self,triangle,i,j):
if self.memo[i][j]!=-1:
return self.memo[i][j]
if i==len(triangle)-1:
return triangle[i][j]
else:
left = self.find(triangle,i+1,j)
right = self.find(triangle,i+1,j+1)
self.memo[i][j] = min(left,right)+triangle[i][j]
return self.memo[i][j]
leetcode 300: 最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
- 状态函数
f(i)为以第i个数字结尾时对应的最大长度,线性动态规划。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n <=1:return n
res = 0
dp = [1] * n
for i in range(1,n):
for j in range(0,i):
if nums[i] > nums[j]:
dp[i] = max(dp[j]+1,dp[i])
res = max(res,dp[i])
return res
leetcode 64: 最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
- 状态转移:
f(i,j) = min(f(i,j-1),f(i-1,j))+val[i,j],需要注意的是要判断其左边或者上面的元素是否存在。
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
if not len(grid) or not len(grid[0]):
return 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if i == 0 and j == 0 : continue
elif i == 0 : grid[i][j] = grid[i][j-1] + grid[i][j]
elif j == 0 : grid[i][j] = grid[i-1][j] + grid[i][j]
else:
grid[i][j] = min(grid[i][j-1],grid[i-1][j])+grid[i][j]
return grid[-1][-1]
*leetcode 174: 地下城游戏
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
-2(K) -3 3
-5 -10 1
10 30 -5 (P)
说明:
骑士的健康点数没有上限。
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
- 如果沿正方向推的话,需要考虑初值是多少的问题,还需要注意在路上健康值不能小于零,比较麻烦。不妨从最后的位置P出发,沿着上方或者左方移动到K点。而在位置P处,如果
dungeon[p]小于0,则需要1-dungeon[p]的健康值才能到达此处,如果大于等于0则只需要1健康值. - 在设定了
[M-1,N-1]处的健康值之后,可以先反推出最后一行以及最后一列每个位置需要的健康值(都是只有一条路径) - 最后再对中间的位置进行迭代,状态转移方程为
f(i,j)=min(f(i+1,j),f(i,j+1))-dungeon[i,j]。注意在进行状态转移的时候也需要考虑相减后健康值如果小于0时,说明[i,j]处为正值,其位置上健康值只需要有1即可
class Solution:
def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:
if not len(dungeon) or not len(dungeon[0]):
return 0
M,N = len(dungeon),len(dungeon[0])
dp = [[None for _ in range(N)] for __ in range(M)]
dp[-1][-1] = 1 if dungeon[-1][-1] >= 0 else 1 - dungeon[-1][-1]
for j in range(N-2,-1,-1):
tmp = dp[M-1][j+1] - dungeon[M-1][j]
dp[M-1][j] = 1 if tmp <= 0 else tmp
#tmp <=0 说明在在上一个位置[M-1,j]正值,在其位置上只需要1点健康值
for i in range(M-2,-1,-1):
tmp = dp[i+1][N-1] - dungeon[i][N-1]
dp[i][N-1] = 1 if tmp <= 0 else tmp
for i in range(M-2,-1,-1):
for j in range(N-2,-1,-1):
tmp = min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j]
dp[i][j] = 1 if tmp <=0 else tmp
return dp[0][0]
