*offer 12: 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
提示:
1 <= board.length <= 200
1 <= board[i].length <= 200
- DFS + 回溯,对矩阵的每一个节点做深度优先遍历去匹配字符串,结合一个矩阵visited表明位置是否已经被访问过(更方便的方法,直接对原矩阵进行值修改,要注意完成dfs之后要进行还原)。
- DFS终止条件:索引越界、对应的字符不匹配、位置已经被访问过,返回false;
- 当每个字符都完成匹配后返回true。
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
def dfs(i,j,k):
if not 0 <=i<len(board) or not 0<=j<len(board[0]) or board[i][j]!=word[k]:
return False
if k == len(word)-1: return True
#满足条件 设定为visited ,并遍历其四个方向
tmp,board[i][j] = board[i][j],'/'
res = dfs(i-1,j,k+1) or dfs(i+1,j,k+1) or dfs(i,j-1,k+1) or dfs(i,j+1,k+1)
board[i][j] = tmp
return res
for i in range(len(board)):
for j in range(len(board[0])):
if dfs(i,j,0) : return True
return False
offer 13: 机器人的运动范围
[中等]地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 100
0 <= k <= 20
- 思路一 BFS 队列存储坐标
(x,y),每次出队列后访问其右下元素(该问题对称性),判断其元素是否满足条件(在矩阵内以及数字和小于k),当满足条件时在将其右下元素插入队列 - 相关库:
queue对应常用函数:put(),get(),qsize(),empty()
class Solution:
def movingCount(self, m: int, n: int, k: int) -> int:
def num_sum(n):
res = 0
while n:
res += n%10
n = n // 10
return res
from queue import Queue
que = Queue()
que.put((0,0))
res = set()
while not que.empty():
cur_x,cur_y = que.get()
if (cur_x,cur_y) not in res and 0<=cur_x<m and 0<=cur_y<n and num_sum(cur_x)+num_sum(cur_y)<=k:
res.add((cur_x,cur_y))
que.put((cur_x+1,cur_y))
que.put((cur_x,cur_y+1))
return len(res)
- DFS,递归
class Solution:
def movingCount(self, m: int, n: int, k: int) -> int:
self.visited = set()
def num_sum(n):
res = 0
while n:
res += n%10
n = n // 10
return res
def dfs(x,y):
if 0 <= x < m and 0 <= y < n and (x,y) not in self.visited and num_sum(x)+num_sum(y)<=k:
self.visited.add((x,y))
dfs(x+1,y)
dfs(x,y+1)
dfs(0,0)
return len(self.visited)
*leetcode 401: 二进制手表
二进制手表顶部有 4 个 LED 代表小时(0-11),底部的 6 个 LED 代表分钟(0-59)。
每个 LED 代表一个 0 或 1,最低位在右侧。
给定一个非负整数 n 代表当前 LED 亮着的数量,返回所有可能的时间。
案例:
输入: n = 1 返回: [“1:00”, “2:00”, “4:00”, “8:00”, “0:01”, “0:02”, “0:04”, “0:08”, “0:16”, “0:32”]
注意事项:
输出的顺序没有要求。 小时不会以零开头,比如 “01:00” 是不允许的,应为 “1:00”。 分钟必须由两位数组成,可能会以零开头,比如 “10:2” 是无效的,应为 “10:02”。
- 回溯加剪枝,判断当不满足时间的格式要求时直接结束当前的回溯。使用visited存储对应位的选择情况,dfs函数携带指示已选择的个数step以及当前所在的位置pos,当该值等于要求的num时将其加入结果列表。
- dfs函数体:根据参数step判定是否中止,如果未中止,从start开始遍历到最大长度,将其中的每一位设为本次的选择结果,然后递归执行dfs,判断下一个位置。
class Solution:
def __init__(self):
self.ans = []
self.nums = [1,2,4,8,1,2,4,8,16,32]
self.visited = [0 for _ in range(len(self.nums))]
def readBinaryWatch(self, num: int) -> List[str]:
self.dfs(num,0,0)
return self.ans
def dfs(self,num,step,pos):
if step == num:
self.ans.append(self.get_time(self.visited))
return
for i in range(pos,len(self.nums)):
self.visited[i] = 1
if not self.isLeagal(self.visited):
self.visited[i] = 0
continue
self.dfs(num,step+1,i+1)
self.visited[i] = 0
#判断当前已选的时间的有效性
def isLeagal(self,visited):
sum_h = 0
sum_m = 0
for i in range(len(visited)):
if visited[i] == 0:
continue
if i < 4:
sum_h += self.nums[i]
else:
sum_m += self.nums[i]
return 0 <= sum_h < 12 and 0 <= sum_m <60
def get_time(self,visited):
sum_h = 0
sum_m = 0
for i in range(len(visited)):
if visited[i] == 0:
continue
if i < 4:
sum_h += self.nums[i]
else:
sum_m += self.nums[i]
result = "" + str(sum_h) + ":"
if sum_m < 10:
result += "0" + str(sum_m)
else:
result += str(sum_m)
return result
leetcode 784: 字母大小写全排列
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
示例:
输入: S = "a1b2"
输出: ["a1b2", "a1B2", "A1b2", "A1B2"]
输入: S = "3z4"
输出: ["3z4", "3Z4"]
输入: S = "12345"
输出: ["12345"]
注意:
S 的长度不超过12。
S 仅由数字和字母组成。
class Solution:
def dfs(self,S,cur):
if cur == len(S):
self.ans.append("".join(self.path))
return
if S[cur].isalpha():
self.path.append(S[cur].upper()) if S[cur].islower() else self.path.append(S[cur].lower())
self.dfs(S,cur+1)
self.path.pop()
self.path.append(S[cur])
self.dfs(S,cur+1)
self.path.pop()
def letterCasePermutation(self, S: str) -> List[str]:
self.ans = []
self.path = []
self.dfs(S,0)
return self.ans
Leetcode 17: 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
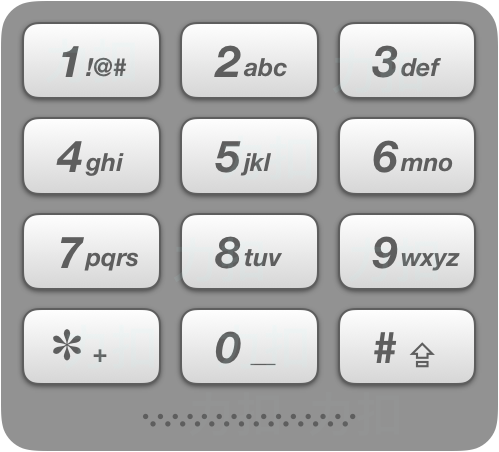
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明: 尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
class Solution:
def __init__(self):
self.key_map = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'}
self.ans = []
self.path = []
def letterCombinations(self, digits: str) -> List[str]:
if not digits:return []
self.dfs(digits,0)
return self.ans
def dfs(self,digits,pos):
if pos == len(digits):
self.ans.append("".join(self.path))
return
chars = self.key_map[digits[pos]]
for c in chars:
self.path.append(c)
self.dfs(digits,pos+1)
self.path.pop()
*leetcode 131: 分割回文串
[中等]给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
- 再递归函数体内,从当前位置pos开始,分别访问不同长度的序列,验证其是否回文,如果是的话移动位置pos到序列尾,将该序列加入path,并进入递归函数检查其接下来的序列。当不满足条件时记得path要pop刚才的序列。
class Solution:
def __init__(self):
self.ans = []
self.path = []
def partition(self, s: str) -> List[List[str]]:
if not s:return []
self.dfs(s,0)
return self.ans
def dfs(self,S,pos):
if pos == len(S):
self.ans.append(list(self.path))
for i in range(pos+1,len(S)+1):
if S[pos:i] == S[pos:i][::-1]:
self.path.append("".join(S[pos:i]))
self.dfs(S,i)
self.path.pop()
leetcode 45: 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
class Solution:
def __init__(self):
self.ans = []
self.path = []
self.visited = []
def permute(self, nums: List[int]) -> List[List[int]]:
self.visited = [0 for _ in range(len(nums))]
self.dfs(nums,0)
return self.ans
def dfs(self,nums,pos):
if pos == len(nums):
self.ans.append(list(self.path))
for i in range(len(nums)):
if self.visited[i]!=1:
self.path.append(nums[i])
self.visited[i] = 1
self.dfs(nums,pos+1)
self.path.pop()
self.visited[i] = 0
leetcode 47: 全排列2
给定一个可包含重复数字的序列,返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
- 在递归体,循环中添加检测是不是重复数字,重复的在同一层只执行一次。
class Solution:
def __init__(self):
self.ans = []
self.path = []
self.visited = []
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
self.visited = [0 for _ in range(len(nums))]
self.dfs(nums,0)
return self.ans
def dfs(self,nums,pos):
unique_num = set()
if pos == len(nums):
self.ans.append(list(self.path))
for i in range(len(nums)):
if self.visited[i]!=1 and nums[i] not in unique_num:
unique_num.add(nums[i])
self.path.append(nums[i])
self.visited[i] = 1
self.dfs(nums,pos+1)
self.path.pop()
self.visited[i] = 0
leetcode 77: 组合
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
- 为避免重复,可以设定后面选择的数字一定比前面大,当选择的数字个数达到k个时append进结果列表。
class Solution:
def __init__(self):
self.ans = []
self.path = []
def combine(self, n: int, k: int) -> List[List[int]]:
self.dfs(n,k,1)
return self.ans
def dfs(self,n,k,pos):
if len(self.path) == k:
self.ans.append(list(self.path))
for i in range(pos,n+1):
self.path.append(i)
self.dfs(n,k,i+1)
self.path.pop()
leetcode 39: 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。 解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
- 可重复选,
pos不需要加一,通过target的值来判断是否满足条件中止回溯。
class Solution:
def __init__(self):
self.ans = []
self.path = []
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
candidates = sorted(candidates)
self.dfs(candidates,0,target)
return self.ans
def dfs(self,candidates,pos,target):
if target == 0:
self.ans.append(list(self.path))
return
elif target < 0:
return
for i in range(pos,len(candidates)):
if candidates[i] > target:
continue
self.path.append(candidates[i])
self.dfs(candidates,i,target-candidates[i])
self.path.pop()
leetcode 40: 组合总和2
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。 解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
- 相对上一题,需要注意的点:
- 每个数字只能用一次,但数组里会有重复数字,可以先排序一下。在同一层的回溯中,相同的数字只访问一次
class Solution:
def __init__(self):
self.ans = []
self.path = []
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates = sorted(candidates)
self.dfs(candidates,0,target)
return self.ans
def dfs(self,candidates,pos,target):
unique_nums = set()
if target == 0:
self.ans.append(list(self.path))
return
elif target < 0:
return
if pos >= len(candidates) or candidates[pos]>target:
return
for i in range(pos,len(candidates)):
if candidates[i] > target:
continue
if candidates[i] in unique_nums:
continue
unique_nums.add(candidates[i])
self.path.append(candidates[i])
self.dfs(candidates,i+1,target-candidates[i])
self.path.pop()
leetcode 216:组合总和3
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。 解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
class Solution:
def __init__(self):
self.ans = []
self.path = []
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
self.dfs(1,k,n)
return self.ans
def dfs(self,pos,k,target):
if len(self.path)==k and target == 0:
self.ans.append(list(self.path))
return
if target <= 0 or pos > 9 :
return
for i in range(pos,10):
if pos > target:break
self.path.append(i)
self.dfs(i+1,k,target-i)
self.path.pop()
*leetcode 78:子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
- 方法一 迭代法 设定初始输出集合为空,每一步向该集合中添加新的整数,生成新的子集。按序添加,不会存在重复的情况。只要上一步的子集不存在重复,则都添加同样的元素后也不会重复
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for i in nums:
res += [r+[i] for r in res]
return res
- 方法二 回溯 需要遍历数组的长度,分别生成不同长度的子集。
class Solution:
def __init__(self):
self.ans = []
self.path = []
def subsets(self, nums: List[int]) -> List[List[int]]:
for i in range(len(nums)+1):
self.dfs(nums,0,i)
return self.ans
def dfs(self,nums,pos,k):
if len(self.path) == k:
self.ans.append(list(self.path))
for i in range(pos,len(nums)):
self.path.append(nums[i])
self.dfs(nums,i+1,k)
self.path.pop()
- 方法三 二进制掩码法
示例: 对长度3的nums数组[1,2,3],可以生成从000到111的二进制掩码,然后根据掩码字符串和nums数组对应的位置判断是否取该数字。
掩码生成
bin(1) = "0b1"
bin(8) = "0b1000"
直接使用bin函数生成的掩码没用自动填充0,为生成掩码,可以*或*操作一个高一位的二进制值1000(2^3),而后取后三位,从而完成了掩码的对齐。
nth_bit = 1 << 3
bin(1 | nth_bit) = "0b1001"
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
nth_bit = 1 << n
for i in range(2**n):
mask = bin( i | nth_bit)[3:]
res.append([nums[j] for j in range(n) if mask[j]=='1'])
return res
leetcode 90: 子集2
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
- 核心在于去重,对排好序的数组,如果当前元素和上一个元素相同且上一个元素在本次递归中没有使用,则需要进行剪枝操作。
class Solution:
def __init__(self):
self.ans = []
self.path = []
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
self.visited = [0 for _ in range(len(nums))]
nums = sorted(nums)
for i in range(len(nums)+1):
self.dfs(nums,0,i)
return self.ans
def dfs(self,nums,pos,k):
if len(self.path) == k:
self.ans.append(list(self.path))
return
for i in range(pos,len(nums)):
if i > 0 and nums[i] == nums[i-1] and self.visited[i-1] == 0:
continue
self.path.append(nums[i])
self.visited[i] = 1
self.dfs(nums,i+1,k)
self.visited[i] = 0
self.path.pop()
leetcode 79: 单词搜索
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board =
[
['A','B','C','E'],
['S','F','C','S'],
['A','D','E','E']
]
给定 word = "ABCCED", 返回 true
给定 word = "SEE", 返回 true
给定 word = "ABCB", 返回 false
提示:
board 和 word 中只包含大写和小写英文字母。
1 <= board.length <= 200
1 <= board[i].length <= 200
1 <= word.length <= 10^3
- 同第一题
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
for i in range(len(board)):
for j in range(len(board[0])):
ans = self.dfs(board,word,i,j,0)
if ans:return True
return False
def dfs(self,board,word,i,j,k):
if k == len(word):
return True
if i <0 or i >= len(board) or j <0 or j>=len(board[0]) or board[i][j]!=word[k]:
return False
tmp,board[i][j] = board[i][j], '#'
res = self.dfs(board,word,i-1,j,k+1) or self.dfs(board,word,i+1,j,k+1) or self.dfs(board,word,i,j-1,k+1) or self.dfs(board,word,i,j+1,k+1)
board[i][j] = tmp
return res
*leetcode 200: 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
-
方法一 深度优先搜索 :
- 我们可以将二维网格看成一个无向图,竖直或水平相邻的 1 之间有边相连。
- 为了求出岛屿的数量,我们可以扫描整个二维网格。如果一个位置为 1,则以其为起始节点开始进行深度优先搜索。在深度优先搜索的过程中,每个搜索到的 1 都会被重新标记为 0。
- 最终岛屿的数量就是我们进行深度优先搜索的次数。
class Solution: def numIslands(self, grid: List[List[str]]) -> int: res = 0 for i in range(len(grid)): for j in range(len(grid[0])): if grid[i][j] == '1': res += 1 self.dfs(grid,i,j) return res def dfs(self,grid,i,j): grid[i][j]= '0' directions = [(-1,0),(1,0),(0,-1),(0,1)] for x,y in directions: if 0<=i+x<len(grid) and 0 <= j+y<len(grid[0]) and grid[i+x][j+y]=='1': self.dfs(grid,i+x,j+y) -
方法二 广度优先 在对每个位置进行遍历时,若其值为1,则标记为0,而后将该点耸入队列,队列弹出元素时再验证其值。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
from collections import deque
res = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
res += 1
neighbors = deque([(i,j)])
while neighbors:
cur_x,cur_y = neighbors.popleft()
directions = [(-1,0),(1,0),(0,-1),(0,1)]
for x,y in directions:
if 0<=cur_x+x<len(grid) and 0 <= cur_y+y<len(grid[0]) and grid[cur_x+x][cur_y+y]=='1':
neighbors.append((cur_x+x,cur_y+y))
grid[cur_x+x][cur_y+y]='0'
return res
leetcode 130: 被围绕的区域
给定一个二维的矩阵,包含 ‘X’ 和 ‘O’(字母 O)。
找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
示例:
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
解释:
被围绕的区间不会存在于边界上,换句话说,任何边界上的 ‘O’ 都不会被填充为 ‘X’。 任何不在边界上,或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
- 思路:从边缘位置开始DFS,能遍历到的位置均为’O’,其他的位置为’X’。
class Solution:
def solve(self, board: List[List[str]]) -> None:
for i in range(len(board)):
for j in range(len(board[0])):
if i ==0 or i == len(board)-1 or j == 0 or j == len(board[0])-1:
self.dfs(board,i,j)
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j]=='#':
board[i][j]='O'
else:
board[i][j]='X'
def dfs(self,board,i,j):
if 0 <= i < len(board) and 0 <= j < len(board[0]) and board[i][j]=='O':
board[i][j] = '#'
for x,y in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:
self.dfs(board,x,y)
leetcode 417: 太平洋大西洋水流问题
给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。
规定水流只能按照上、下、左、右四个方向流动,且只能从高到低或者在同等高度上流动。
请找出那些水流既可以流动到“太平洋”,又能流动到“大西洋”的陆地单元的坐标。
提示:
输出坐标的顺序不重要 m 和 n 都小于150
示例:
给定下面的 5x5 矩阵:
太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * 大西洋
返回:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).
- 思路 顺流的方法从中间到两边不太好做,可以用逆流的思路,分别计算出从太平洋以及大西洋逆流能到的位置,然后两个都能到的即为最终的结果。
class Solution:
def pacificAtlantic(self, matrix: List[List[int]]) -> List[List[int]]:
if not matrix or not matrix[0]: return []
self.m,self.n = len(matrix),len(matrix[0])
self.matrix = matrix
res1,res2 = set(),set()
for i in range(self.m):
self.dfs(i,0,res1)
for j in range(self.n):
self.dfs(0,j,res1)
for i in range(self.m):
self.dfs(i,self.n-1,res2)
for j in range(self.n):
self.dfs(self.m-1,j,res2)
return res1 & res2
def dfs(self,i,j,cur_res):
cur_res.add((i,j))
for x,y in [[1,0],[0,1],[-1,0],[0,-1]]:
temp_i = i + x
temp_j = j + y
if 0 <= temp_i < self.m and 0<= temp_j < self.n and self.matrix[i][j] <= self.matrix[temp_i][temp_j] and (temp_i,temp_j) not in cur_res:
self.dfs(temp_i,temp_j,cur_res)
*leetcode 207: 课程表
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
提示:
输入的先决条件是由 边缘列表 表示的图形,而不是 邻接矩阵 。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
1 <= numCourses <= 10^5
- 拓扑排序 DAG图的判定
- 统计课程安排图中每个节点的入度,生成 入度表 indegrees。
- 借助一个队列 queue,将所有入度为 0 的节点入队。当 queue 非空时,依次将队首节点出队,在课程安排图中删除此节点 pre:并不是真正从邻接表中删除此节点 pre,而是将此节点对应所有邻接节点 cur 的入度 −1,即 indegrees[cur] -= 1。
- 当入度 −1后邻接节点 cur 的入度为 0,说明 cur 所有的前驱节点已经被 “删除”,此时将 cur 入队。 在每次 pre 出队时,执行 numCourses–;
- 若整个课程安排图是有向无环图(即可以安排),则所有节点一定都入队并出队过,即完成拓扑排序。换个角度说,若课程安排图中存在环,一定有节点的入度始终不为 0。
- 因此,拓扑排序出队次数等于课程个数,返回 numCourses == 0 判断课程是否可以成功安排。
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
indegrees = [0 for _ in range(numCourses)]
adjacency = [[] for _ in range(numCourses)]
from collections import deque
queue =deque()
for cur,pre in prerequisites:
indegrees[cur] += 1
adjacency[pre].append(cur)
#找到初始入度为0的所有节点送到队列
for i in range(len(indegrees)):
if not indegrees[i]:queue.append(i)
while queue:
pre = queue.popleft()
numCourses -= 1
#pre指向的所有课程入度减一,如果等于零加入到队列中
for cur in adjacency[pre]:
indegrees[cur]-=1
if not indegrees[cur]:queue.append(cur)
return numCourses == 0