1 简介
随着图卷积神经网络在近年来的不断发展,其对于图结构数据的建模能力愈发强大。然而现阶段的工作大多针对简单无向图或者异质图的表示学习,对图中边存在方向和类型的特殊图—-多关系图(Multi-relational Graph)的建模工作较少,且大多存在着两个问题:
(1)整体网络模型的过参数化,
(2)仅针对于结点的表示学习。
针对这两个问题,本论文提出了一种基于组合的图卷积神经网络来同时建模结点和边的表示,为了降低大量的边类型带来的参数量,作者采用了向量分解的方式,所有的边类型表示通过一组基向量的线性组合来完成。
2 准备知识
本文主要是对多关系图卷积神经网络的介绍,对于基础的图卷积神经网络可以参考论文[1],在这里只是简单回顾一下图卷积神经网络的做法。
2.1 无向图上的图卷积神经网络
对于无向图 $G=(\cal V,E,X)$,$\cal V$为结点集合,$\cal E$为边的集合,$\cal X\in\Bbb{R}^{|v|\times d}$为每一个节点的$d$维输入特征表示,则一层GCN模型可以表示为: \(H=f(\hat{A}HW)\) 其中$\hat A=\widetilde D^{-\frac{1}{2}}(A+I)\widetilde D^{-\frac{1}{2}}$为归一化的带自环的邻接矩阵,矩阵$\widetilde D$定义为:$\widetilde D = \sum_j(A+I){ij}$。单层GCN模型的参数为$W\in \Bbb R^{d_0\times d_1}$,$f$为激活函数,通过编码每一个结点的一阶邻居结点的信息来得到新的节点表示$H$。为了捕捉图中存在的高阶近邻关系,可以堆叠多层GCN层,其第$k+1$层的表示可以通过聚合第$k$层的节点表示来完成: \(H^{k+1} = f(\hat AH^k W^k)\) 其中$k$为GCN的层数,$W^k\in \Bbb R^{d_k\times d{k+1}}$为该层的模型参数,$H^0=\cal X$为初始的节点特征表示。
2.2多关系图上的图卷积
多关系图相较于无向图多出了边的方向以及类型的特征,在做GCN的时候如何融入这些信息便是多关系图卷积的难点,同样是多关系图卷积的核心。接下来简单介绍下基于论文[2]的多关系图卷积模型。
对于给定的多关系图$G=(\cal V,R,E,X)$,$V$为结点集合,$R$为关系的类别集合,$(u,v,r)∈\cal E$代表从结点$u$出发到结点$v$类别为$r$的边,同样有$(v,u,r^{-1} )∈G$。$\cal X\in \Bbb R^{|V|\times d_0 }$为输入的$d_0$维节点特征,其GCN模型定义为: \(H^{k+1}=f(\hat A H^k W_r^k)\) 其中$W_r^k$为与边类型$r∈R$相关的参数矩阵,对应不同类别的边连接的结点,在进行GCN信息聚合时需要使用不用的参数矩阵,由此就产生了过参数化的问题[3]。而在论文[2]中,为了缓解这一问题,将参数矩阵$W_r^k$进行了分解,通过基向量组合和对角矩阵组合两种方式降低了参数量,有兴趣的可以阅读一下。
3 模型介绍
本论文的核心也在于解决过参数化的问题,通过引入边类型的表示向量来取代原本根据不同边类型的参数矩阵$W_r^k$,然后通过节点向量和边类型向量的组合操作来综合结点和边的表示,从而把线性变换的参数矩阵数量变少。为进一步处理边类型过多的问题,作者通过基向量组合的方式来表示边,进一步优化了参数的复杂度。
3.1 结点–边类型信息融合
对于给定的多关系图$G=(\cal V,R,E,X,Z)$,其$\cal V,R,E,X$的定义均与之前相同,在本文中引入了边类型的表示特征$\cal Z∈\Bbb R^{|R|∗d_0}$,为了联合结点和边的特征,本文参照了知识图谱领域的做法,通过实体关系组合操作来完成信息的融合: \(e_o = \phi(e_s,e_r)\) 其中$s,r,o$ 分别代表了知识图谱中的主体、关系和目标,$\phi(\cdot)$为特定的组合操作符,$e(\cdot)$为对应的向量表示,目标的表示$e_o$可以通过主体和关系的表示$e_s,e_r$结合来得到。
在这篇论文中,为了保证不引入额外的参数,增大复杂度,只采用了无参数的操作,比如减法、点乘以及循环相关运算:
- 减法:$\phi(e_s,e_r) = e_s- e_r$.
- 点乘:$\phi(e_s,e_r) = e_s * e_r$.
- 循环相关性[4]:$\phi(e_s,e_r)k = \sum{i=0}^{d-1}e_{s,i}e_{r,k+i}\mod d$.
由此,把结点和边的表示综合起来。
3.2 结点和边的表示更新
在完成了结点和边类型的信息融合之后,就可以通过参数量较少的参数矩阵来更新结点和边类型的表示,对结点特征表示的更新为GCN模型的编码: \(h_v^{k+1} = f(\sum_{(u,v) \in \cal N(v)}W_{\lambda(r)}^k\phi(h_u^k,h_r^k))\) 其中$h_u^k,h_r^k$分别为第$k$层的结点和边类型的特征表示,在第一层GCN有$h_u^0=\cal X,h_r^0=\cal Z$。$W_{\lambda(r)}^k$为第$k$层的参数矩阵,因为在组合操作$\phi(\cdot)$中已经完成了对边的类别信息的编码,参数矩阵W不需要根据类别来设定,而是根据边具有的不同方向来分开处理:
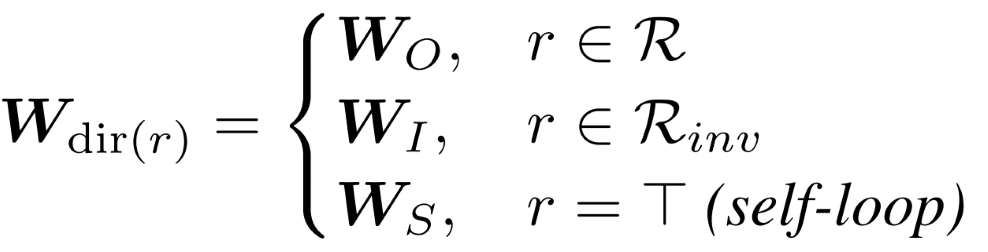
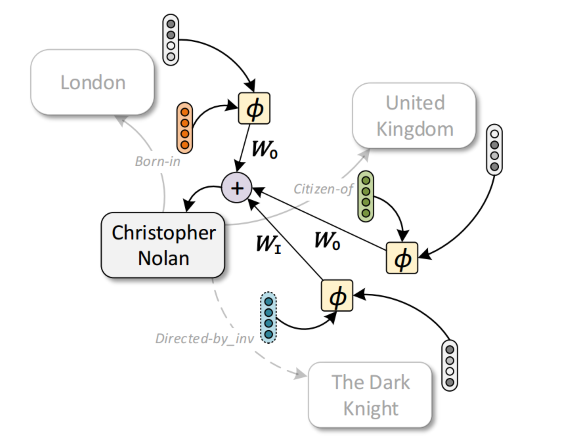
其结点表示更新的过程如图所示:邻居节点的表示结合边类型的表示来促进中间结点的表示更新:
同时,每一层也用一个线性变换完成边类型表示的更新: \(h_r^{k+1} = W_{rel}^kh_r^{k}\) 由此通过多层的GCN模型可以获得最终的结点和边类型的表示,根据下游任务的不同可以设定不同的损失来优化模型。
3.3 边类型表示的分解
类似于论文[2]中对权重矩阵的分解,这篇论文是对边类型的向量表示分解,通过一组基向量$v$来线性组合构建边类型的向量表示$z_r$,基向量维度和节点表示向量维度相同,通过$\cal B$个基向量构造$|R|$种类型边的表示: \(\cal z_r = \sum_{b=1}^{\cal B}\alpha_{br}v_b\) $\alpha_{br}\in \Bbb R$为权重因子。
4 实验
作者分别在链接预测、节点分类和图分类三个任务上进行了测试,数据集的基本信息如下:
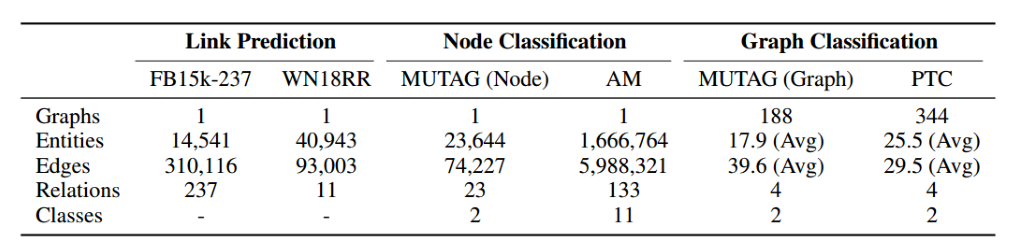
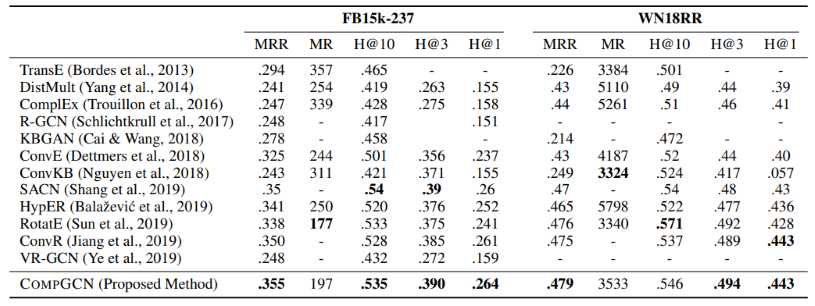
在链接预测的任务上分别测试了多种无参的融合方式的效果,在不同的数据集上,基于不同的融合方式的效果还是比较好的,另外随着知识图谱领域的发展,本方法还可以结合新的融合方式,也可以促进其效果。
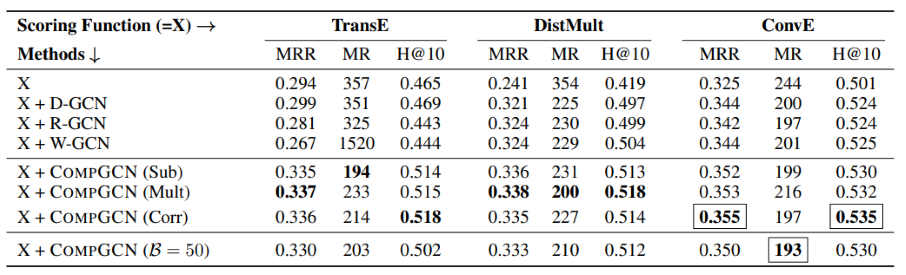
接着进行了基向量维度的实验,相对于不使用基向量的方法,使用基向量的方法能有效地减小参数量而保证性能。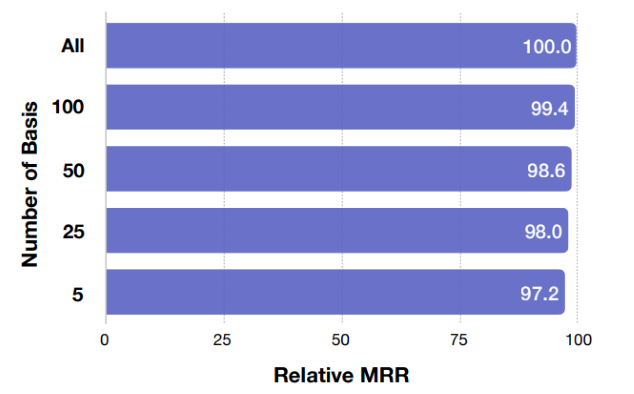
然后作者又进行了结点和图的分类任务,效果也是比较好的,融入边的信息确实能有不错的提升。
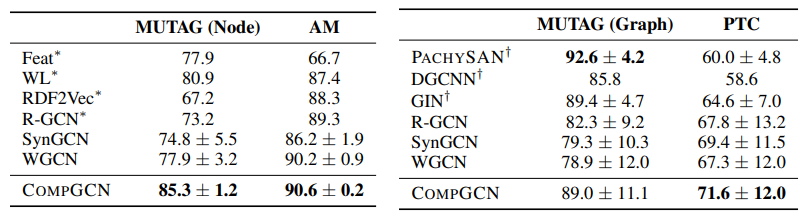
5. 总结
该文章结合了知识图谱领域的特征融合方法设定了组合操作,来联合的学习结点和边类型的表示,在缩小参数量的基础上同样完成了边类型的表示,并通过大量的实验验证了模型的有效性。最后作者还推导了其模型是对其他模型的泛化,很多之前的工作都可以看作该模型的特例。
参考论文
[1] Semi-supervised Classification With Graph Convolutional Networks .
[2] Modeling Relational Data with Graph Convolutional Networks .
[3] Encoding Sentences with Graph Convolutional Networks for Semantic Role Labeling .
[4] Holographic embeddings of knowledge graphs.