1 简介
本文着眼于对Weisfeiler-Lehman算法(WL Test)和WL-GNN模型的分析,针对于WL测试以及WL-GNN所不能解决的环形跳跃连接图(circulant skip link graph)进行研究,并提出了一种基于相对池化的方法,有助于GNN学习到结点之间的相对关系,该方法可以较好地融入到较为通用的神经网络模型中(如CNN、RNN等),使得WL-GNN具有更强大的表征能力。
2 准备知识
2.1 WL Test及其问题
Weisfeiler-Lehman如下所示:
对于任意的节点$v_i\in G$:
- 获取节点${v_i }$所有的邻居节点$j$的特征${v_j }$
- 更新该节点的特征 ${v_i } = hash{\sum_j h_{v_j}}$ ,其中$hash$是一个单射函数$x$不同则$f(x)$一定不同)
重复以上步骤$K$次直到收敛。
其一次迭代过程如下图所示:
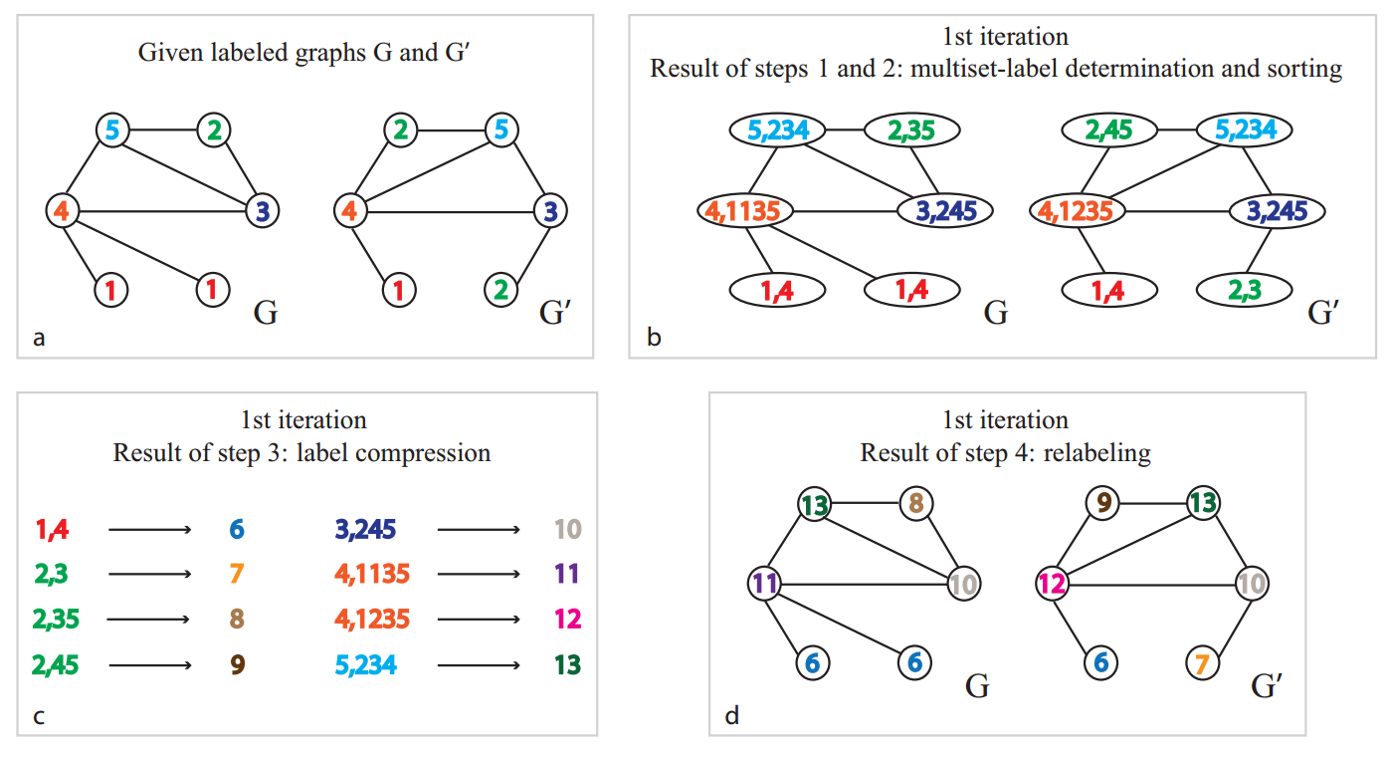
经过一次迭代后我们得到了新的标签分布:

事实上,Weisfeiler-Lehman算法在大多数图上会得到一个独一无二的特征集合,这意味着图上的每一个节点都有着独一无二的角色定位(例外在于网格,链式结构等等)。因此,对于大多数非规则的图结构,得到的特征可以作为图是否同构的判别依据,也就是WL Test,通过统计稳定后label的分布来判定两张图是否同构。
但在WL test中存在一个问题:在结点聚合其邻居信息的时候只是根据其标签特征,而不考虑其位置或者结点编号信息,其节点表示特征无法区分该结点连接的是同一个结点或者是具有相同特征表示的不同节点。如下图己烷($C_6H_{14}$)的图结构:
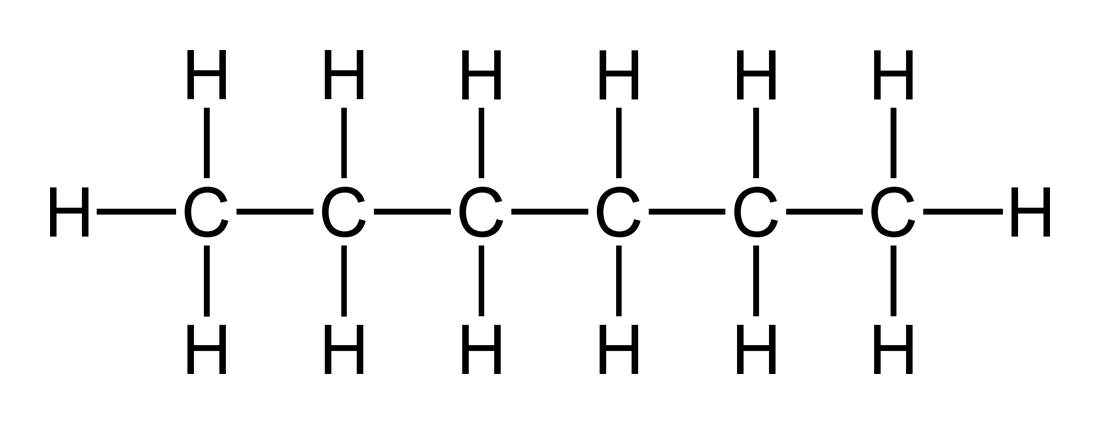
在第一轮WL test中,处于中间的四个C原子具有相同的表示(它们无法判断具体所处的位置,只知道周围有两个C原子和两个H原子),当然该情况可以通过多次的WL test过程来改善,处于左右两端的C原子可以学习到自身处于C链的外层,而随着WL test的迭代,这种位置信息可以逐渐传到中间的C原子表示中(如在第二轮迭代中,第二个C原子会聚合第一个碳原子的结点信息,从而具有一定的位置表征能力)。
而对于更为复杂的结构如环己烷($C_6H_{12}$),无论经过多少轮的WL test迭代,C原子都具有相同的特征表示。
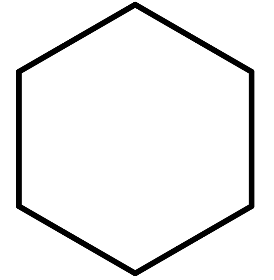
可以看出,当WL test的迭代次数过少或者图中存在复杂的环形结构时,WL test并不能获取到足够有效的结点和图的表征。
而接下来引入一个更为极端的例子:
定义 环形跳跃连接图[Circulant Skip Links (CSL) graphs]:\(\cal{G}_{skip}(M,R)\)代表有${0,1,…,M-1}$结点且其边构成环形以及跳跃连接的无向且度为4的标准图,且$R<M-1$。对其环形结构,对$j\in {0,…,M-2}$有${j,j+1}\in E$且${M-1,0}\in E$。而对其跳跃连接,定义$s_1 =0 , s_{i+1} = (s_i + R) mod M$且${s_i,s_{i+1}\in E}$。
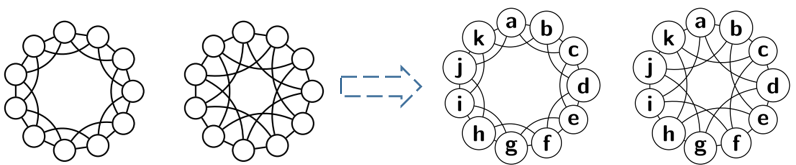
对于$M=11,R={2,3}$的CSL图如下图。
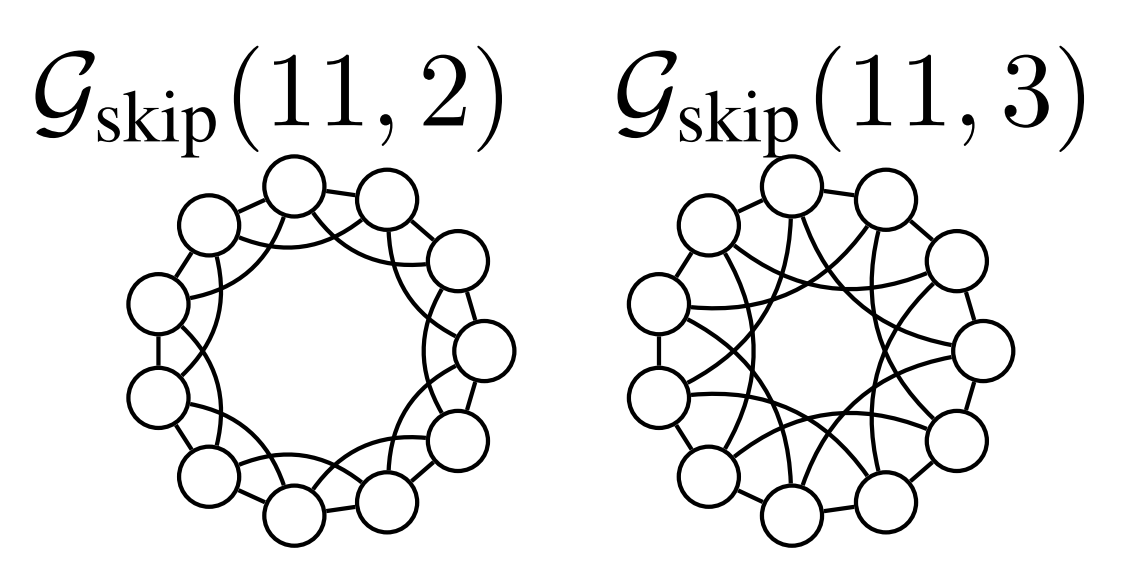
面对这样的图结构,WL test完全失去了判断能力。
2.2 图神经网络(Graph Neural Network)
依其名,对图进行处理的神经网络,对于给定数据集大小为$N$的具有不同大小的图$G_1 ,G_2 ,…,G_N$(每个图可能会有对应的结点/边特征),都有与之对应的标签/值:$y_1,y_2,…,y_N$,通过学习一个图函数$f(.;\theta)$来对图$G$进行预测对应的标签/值$y$.
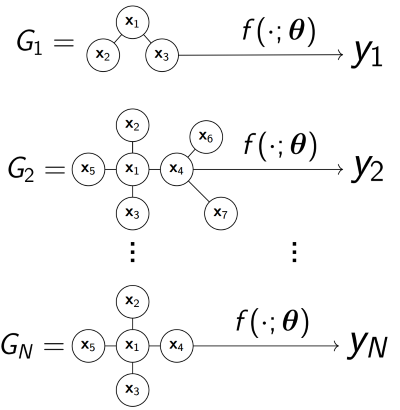
然而,由于图所具有的特殊性,其没有严格的序列关系,其结点顺序改变也会引起近邻矩阵$\boldsymbol A$的改变:
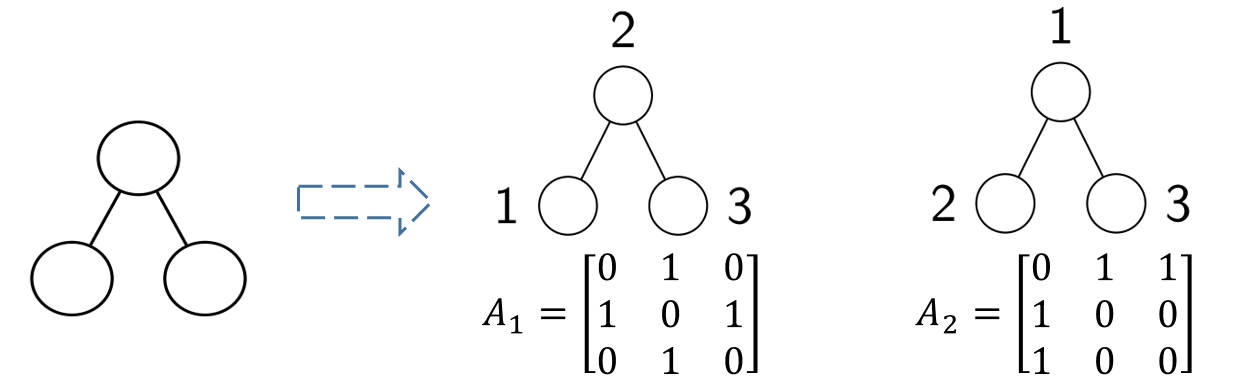
上图为交换了1和2编号的图的近邻矩阵的变化(交换1、2行和1、2列)。而对于具有结点特征的图,还需要对其结点特征矩阵$\boldsymbol X$进行行变换,如下图中对$H_2O$分子的结点编号变换:
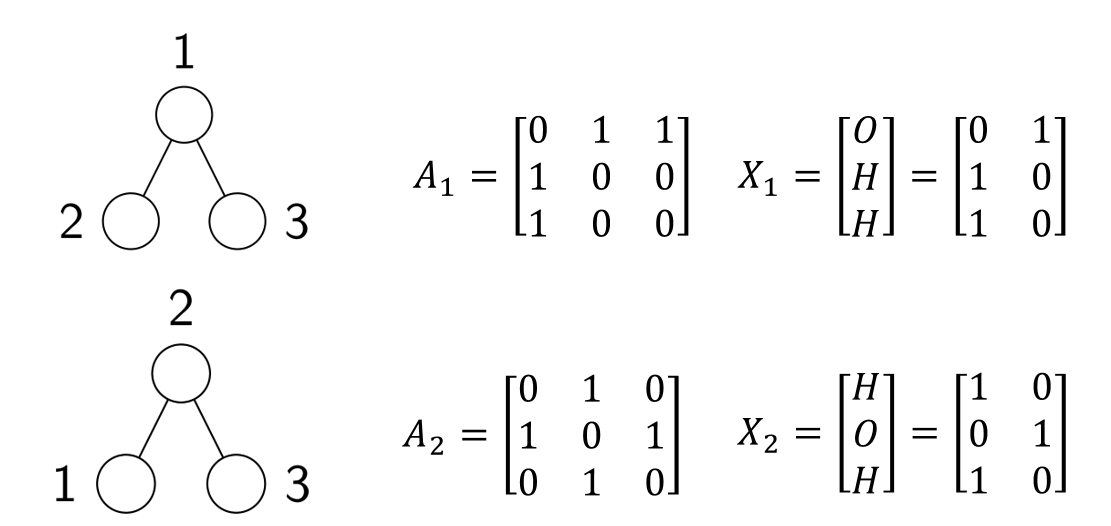
如何保证以不同的顺序送入网络中而得到同样的结果?下面引入交换不变性的概念。
定义 交换不变性[Permutation Invariance]:如果函数$f$对图满足
\[f(\boldsymbol A,\boldsymbol X) = f(\boldsymbol A_{\pi,\pi},\boldsymbol X_\pi)\]则称函数$f$满足交换不变性。
而图神经网络也是在保证交换不变性的原则上将深度学习手段引入图领域,经典的WL-GNN模型遵从以下步骤:
对于给定的结点特征为$\boldsymbol X$的图,所有结点$v \in V$
- 对所有$v \in V$,初始化结点的表示$h_v^{(0)} =x_v$,迭代次数$l=1,2,…,L$,$\phi^{(l)}$为具有交换不变性的函数,$\boldsymbol W^{(l)}$为对应的可学习参数:
- 通过readout函数来综合多层的节点表示得到预测结果: \(\boldsymbol {\hat y} = \psi({\{\boldsymbol h_v^{(0)}}\}_{v\in V},...,{\{\boldsymbol h_v^{(L)}}\}_{v\in V};{\boldsymbol W^{(\psi)}})\)
其权重矩阵都通过SGD来训练。
该模型基于WL test的思想,经证明WL test是此类GNN模型的上界[1]。
而面对WL test解决不了的问题,WL-GNN模型也无法对其进行处理。本文在WL-GNN模型的基础上提出了相对池化,进一步提高了WL-GNN的表征能力。
3 Relational Pooling
核心思想:为WL-GNN模型中的结点添加唯一的ID表示,进而使模型能学习到相对位置信息:
然而,添加了ID表示却破坏了模型的交换不变性,当对ID序列进行变换送入模型中时不能得到一致的结果。为确保对交换不变性的保证,本文使用了一个很朴素的思想:枚举所有可能的交换序列结果,并求其平均来作为最终的输出:
\[\stackrel{=}{f}(\boldsymbol A,\boldsymbol X)=\frac{1}{n!}\sum_{n}\stackrel{\rightarrow}{f}(\boldsymbol A_{\pi,\pi},\boldsymbol X_{\pi})\]其中$\stackrel{=}{.}$为满足交换不变性,而$\stackrel{\rightarrow}{.}$代表对交换敏感。通过这种方法,可以把CNN、RNN等对交换敏感的基础模型应用到图领域。
在RP-GNN模型中定义$\stackrel{\rightarrow}{f}$为:
- 对结点信息添加one-hot ID(对交换敏感)。
- 将上一步结果送入任意GNN模型中。
形式化上,可以得到RP-GNN的最终结构:
\[RPGNN = \stackrel{=}{f}(\boldsymbol A,\boldsymbol X)=\frac{1}{n!}\sum_{n}GNN(\boldsymbol A,CONCAT(\boldsymbol X,\boldsymbol I_{\pi})\]其中$\boldsymbol I_{\pi}$为交换序列的one-hot编码。其计算过程示例如下:
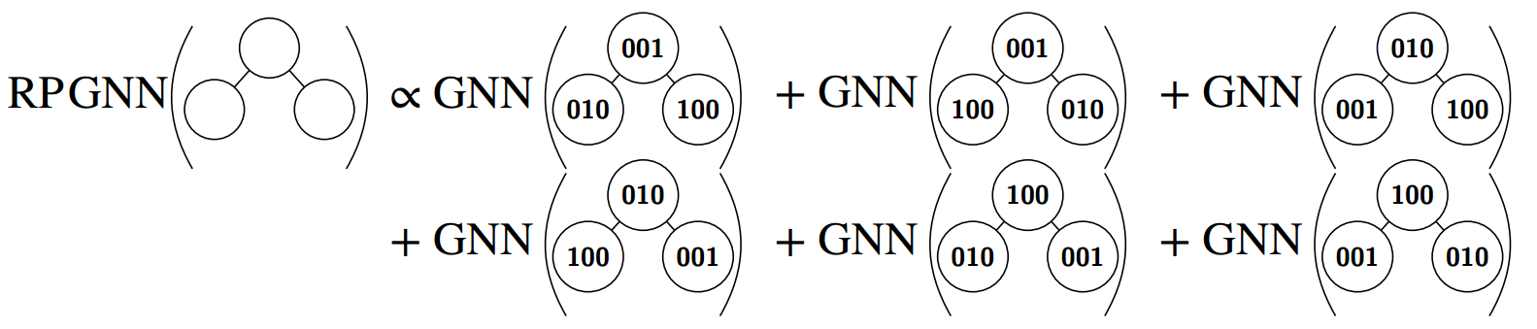
在文中也对RP-GNN的表征能力进行了证明,具体可见论文附录,这里不再详谈。
在图的结点个数$n$增大时,计算其阶乘往往是不现实的,因而本文也提出了两种方法对其计算过程进行优化:
(1)$\pi-SGD$
不计算所有的交换序列结果,通过对所有的交换序列方式($n!$种)进行均匀采样来得到交换序列,然后进行梯度下降优化。

(2)$K-ary$子图
对具有$n$个结点的图,只取其k个结点作为子图,可以结合$\pi-SGD$方法进行模型训练。如图,对一次排序$\pi(1,2,3,4,5) = (3,4,1,2,5)$,取$k=3$的子图。

4 实验
4.1 实验一 CSL图的R值分类
此实验用于从实践角度上证明RP-GNN的表征能力,依照之前的定义构造了数据集来证明RP-GNN相对于WL-GNN的有效性。
数据集构造方式:构造具有41个结点,$R={2,3,4,5,6,9,11,12,13,16}$的CSL图,预测其R所属类别。对所有的十类R值,分别构造15个邻接矩阵(1个为按照CSL图的定义构造,另外14个则是对其进行顺序交换),数据集大小为150。
实验结果如下,对于所有的图,GIN都学到了同样的表示。
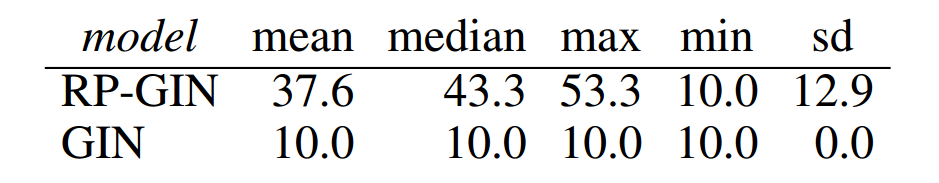
4.2 实验二 分子结构预测
数据集介绍:

实验结果:
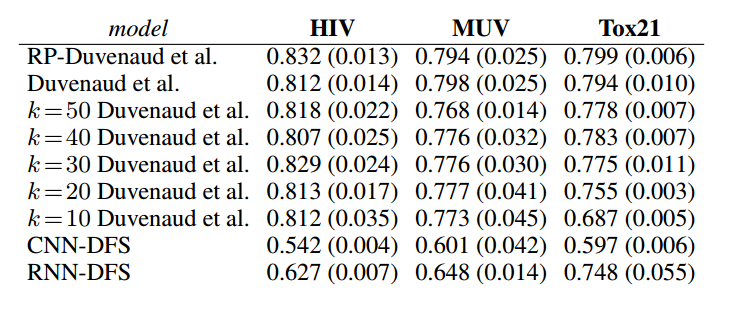
5 总结
本文使用了相对池化对GNN模型进行了改进,提出了一种可加到任意现有模型的相对池化方法,并证明了RP-GNN相对于WL-GNN有着更强的表征能力,最终又提出了有效的计算方法来计算相对池化。