1 Intro
在二分类问题中,通常假设正负类别相对均衡,然而实际应用中类别不平衡的问题,如100, 1000, 10000倍的数据偏斜是非常常见的,比如疾病检测中未患病的人数远超患病的人数,产品质量检测中合格产品数量远超不合格产品等。在检测信用卡欺诈问题中,同样正例的数目稀少,而且正例的数量会随着时间和地点的改变而不断变化,分类器要想在不断变化的正负样本中达到好的检测效果是非常困难的。
由于类别不平衡问题的特性使然,一般常使用于评估分类器性能的在二分类问题中,通常假设正负类别相对均衡,然而实际应用中类别不平衡的问题,如100, 1000, 10000倍的数据偏斜是非常常见的,比如疾病检测中未患病的人数远超患病的人数,产品质量检测中合格产品数量远超不合格产品等。在检测信用卡欺诈问题中,同样正例的数目稀少,而且正例的数量会随着时间和地点的改变而不断变化,分类器要想在不断变化的正负样本中达到好的检测效果是非常困难的。
由于类别不平衡问题的特性使然,一般常使用于评估分类器性能的准确率和错误率可能就不再适用了。因为在类别不平衡问题中我们主要关心数目少的那一类能否被正确分类,而如果分类器将所有样例都划分为数目多的那一类,就能轻松达到很高的准确率,但实际上该分类器并没有任何效果。
所以在这种时候学习的前提往往是采用不同的评估指标。学习机器学习的过程中总不免碰到各种评估指标,刚开始很容易被五花八门的术语绕晕了,所以类别不平衡问题的第一篇先对这些指标进行梳理。毕竟评估指标不明确的话,后面模型的效果好坏也就无从谈起。和错误率可能就不再适用了。因为在类别不平衡问题中我们主要关心数目少的那一类能否被正确分类,而如果分类器将所有样例都划分为数目多的那一类,就能轻松达到很高的准确率,但实际上该分类器并没有任何效果。
所以在这种时候学习的前提往往是采用不同的评估指标。学习机器学习的过程中总不免碰到各种评估指标,刚开始很容易被五花八门的术语绕晕了,所以类别不平衡问题的第一篇先对这些指标进行梳理。毕竟评估指标不明确的话,后面模型的效果好坏也就无从谈起。
Precision(查准率)和Recall(查全率)
首先要介绍几个基本概念:
- True Positive (真正例,TP):实际为正例,预测为正例。
- False Negative (假负例,FN):实际为正例,预测为负例。
- True Negative (真负例,TN):实际为负例,预测为负例。
- False Positive (假正例,FP):实际为负例,预测为正例。
由以上四个概念可以得出模型的混淆矩阵:

查准率和查全率的计算:
\[Precision(查准率) = \frac{TP}{(TP+FP)}\]Precision衡量的是所有被预测为正例的样本中有多少是真正例。但Precision并没有表现有多少正例是被错判为了负例(即FN),举个极端的例子,分类器只将一个样本判为正例,其他所有都判为负例,这种情况下Precision为100%,但其实遗漏了很多正例,所以Precision常和下面的Recall (TPR) 相结合。
\[Recall(查全率) = \frac{TP}{(TP+FN)}\]Recall在某种程度上评估了模型对真实标签为正例的样本的发现能力。
根据$P$和$R$可以计算出评价指标$F$值:
\[F1 score = \frac{2}{\frac{1}{recall}+\frac{1}{precision}}=\frac{2\times precision \times recall}{precision+recall}\]$F$值是一个综合指标,为Precision和Recall的调和平均 (harmonic mean),数值上一般接近于二者中的较小值,因此如果F1score比较高的话,意味着Precision和Recall都较高。
ROC曲线
ROC曲线常用于二分类问题中的模型比较,主要表现为一种真正例率 (TPR) 和假正例率 (FPR) 的权衡。
TPR与FPR
首先介绍正例率和负例率的概念:
True Positive Rate (TPR,真正例率),又称Recall(查全率),Sensitivity(灵敏性)。
\[TPR = \frac{TP}{TP+FN}\]Recall (TPR)衡量的是所有的正例中有多少是被正确分类了,也可以看作是为了避免假负例(FN)的发生,因为TPR高意味着FN低。Recall的问题和Precision正相反,没有表现出有多少负例被错判为正例(即FP),若将所有样本全划为正例,则Recall为100%,但这样也没多大用。
False Positive Rate (FPR,假正例率)
\[FPR = \frac{FP}{TN+FP}\]由混淆矩阵可以看出该指标的着眼点在于负例,意为有多少负例被错判成了正例。在ROC曲线中分别以TPR和FPR作为纵、横轴作图,显示出一种正例与负例之间的“博弈”。
True Negative Rate (TNR,真负例率) 又称Specificity(特异性)
\[TNR = \frac{TN}{TN+FP} = 1-FPR\]Specificity衡量的是所有的负例中有多少是被正确分类了,由于类别不平衡问题中通常关注正例能否正确被识别,Specificity高则FP低,意味着很少将负例错判为正例,即该分类器对正例的判别具有“特异性”,在预测为正例的样本中很少有负例混入。
False Negative Rate (FNR,假负例率)
\[FPR = \frac{FN}{TP+FN}=1-TPR\]由混淆矩阵可以看出该指标的着眼点在于正例,意为有多少正例被错判成了负例。
ROC计算方法
具体方法是在不同的分类阈值 (threshold) 设定下分别以TPR和FPR为纵、横轴作图。假设有P个正例,N个反例,首先拿到分类器对于每个样本预测为正例的概率,根据概率对所有样本进行逆序排列,然后将分类阈值设为最大,即把所有样本均预测为反例,此时图上的点为 (0,0)。然后将分类阈值依次设为每个样本的预测概率,即依次将每个样本划分为正例,如果该样本为真正例,则TP+1,即 ; 如果该样本为负例,则FP+1 。最后的到所有样本点的TPR和FPR值,用线段相连。
- 真实数据与预测的概率值:
y = np.array([1,1,2,2,])
scores = np.array([0.1,0.4,0.35,0.8])
假设label = 1为正例样本,在不同阈值th下预测标签如下表:
| index | real label | probability | th = 0.8 | th = 0.4 | th=0.35 | th=0.1 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0.1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0.4 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0.35 | 0 | 0 | 1 | 1 |
| 3 | 1 | 0.8 | 1 | 1 | 1 | 1 |
由此可以计算出在不同的阈值下的TPR、FPR值:
-
$threshold = 0.8$ 时, \(TPR = \frac{TP}{TP+FN} = \frac{1}{2},FPR = \frac{FP}{FP+TN} = 0\)
-
$threshold=0.4$时,$TPR=\frac{1}{2},FPR=\frac{1}{2}$
-
$threshold=0.35$时,$TPR=1,FPR=\frac{1}{2}$
-
$threshold=0.1$时,$TPR=1,FPR=1$
以FPR为横坐标,TPR为纵坐标绘制ROC曲线如下。
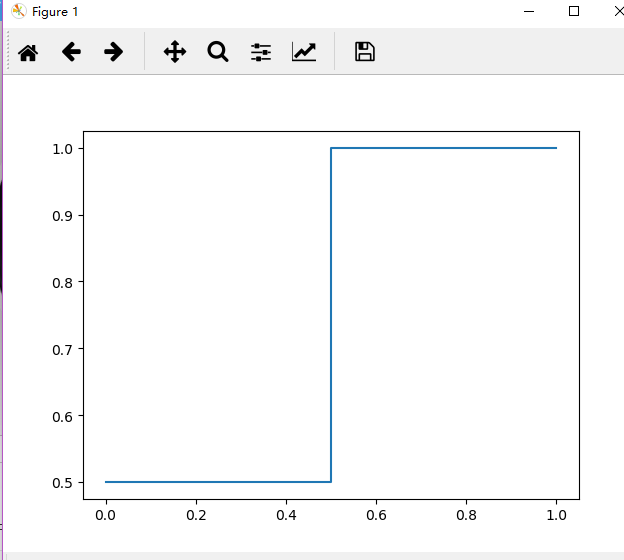
ROC曲线常用于二分类问题中的模型比较,主要表现为一种真正例率 (TPR) 和假正例率 (FPR) 的权衡。由ROC曲线的两个指标, 可以看出,当一个样本被分类器判为正例,若其本身是正例,则TPR增加;若其本身是负例,则FPR增加,因此ROC曲线可以看作是随着阈值的不断移动,所有样本中正例与负例之间的“对抗”。曲线越靠近左上角,意味着越多的正例优先于负例,模型的整体表现也就越好。
ROC曲线的缺点
- 上文提到ROC曲线的优点是不会随着类别分布的改变而改变,但这在某种程度上也是其缺点。因为负例N增加了很多,而曲线却没变,这等于产生了大量FP。像信息检索中如果主要关心正例的预测准确性的话,这就不可接受了。
- 在类别不平衡的背景下,负例的数目众多致使FPR的增长不明显,导致ROC曲线呈现一个过分乐观的效果估计。ROC曲线的横轴采用FPR,根据$FPR=\frac{FP}{FP+TN}$当负例N的数量远超正例P时,FP的大幅增长只能换来FPR的微小改变。结果是虽然大量负例被错判成正例,在ROC曲线上却无法直观地看出来。(当然也可以只分析ROC曲线左边一小段)
举个例子,假设一个数据集有正例20,负例10000,开始时有20个负例被错判:
\[FPR_1 = \frac{20}{20+9980} = 0.002,P_1=\frac{20}{20+20}=0.5\]接着又有20个负例错判:
\[FPR_2=\frac{40}{40+9980}=0.004,P_2=\frac{20}{20+40}=\frac{1}{3}\]在ROC曲线上这个变化是很细微的。而与此同时Precision则从原来的0.5下降到了0.33,在PR曲线上将会是一个大幅下降。
$PR$曲线
PR曲线展示的是Precision vs Recall的曲线,PR曲线与ROC曲线的相同点是都采用了TPR (Recall),都可以用AUC来衡量分类器的效果。不同点是ROC曲线使用了FPR,而PR曲线使用了Precision,因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例,所以在此情况下PR曲线被广泛认为优于ROC曲线。
PR曲线的绘制与ROC曲线类似
使用场景
-
ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。
-
如果有多份数据且存在不同的类别分布,比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同,这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响,则ROC曲线比较适合,因为类别分布改变可能使得PR曲线发生变化时好时坏,这种时候难以进行模型比较;反之,如果想测试不同类别分布下对分类器的性能的影响,则PR曲线比较适合。
-
如果想要评估在相同的类别分布下正例的预测情况,则宜选PR曲线。
-
类别不平衡问题中,ROC曲线通常会给出一个乐观的效果估计,所以大部分时候还是PR曲线更好。
-
最后可以根据具体的应用,在曲线上找到最优的点,得到相对应的precision,recall,f1 score等指标,去调整模型的阈值,从而得到一个符合具体应用的模型。